1. 树的刷题顺序
| 题目分类 | 题目编号 |
|---|---|
| 树与递归 | 100、222、101、226、437、563、617、508、572、543、654、687、87 |
| 树的层次遍历 | 102、429、690、559、662、671、513、515、637、103、107、257、623、653、104、111、112、113、129、404、199、655、116、117 |
| 树的前序遍历 | 144、589 |
| 树的前序序列化 | 606、331、652、297、449 |
| 树的后序遍历 | 145、590 |
| 树的中序遍历与二叉搜索树 | 94、700、530、538、230、98、173、669、450、110、95、108、109 |
| 重构二叉树 | 105、106 |
| 二叉树的展开 | 114 |
| 最近公共祖先 | 235、236 |
| Morris中序遍历 | 501、99 |
| 四叉树 | 558、427 |
2. 树板块知识点归纳总结
2.1. 树的基本概念
树是由结点或顶点和边组成的(可能是非线性的)且不存在着任何环的一种数据结构。没有结点的树称为空(null或empty)树。一棵非空的树包括一个根结点,还(很可能)有多个附加结点,所有结点构成一个多级分层结构

关于“树”,还有三个比较相似的概念:高度(Height)、深度(Depth)、层(Level)。它们的定义是这样的
节点的高度:节点到叶子节点的最长路径(边数)
节点的深度:根节点到这个节点所经历的边的个数
节点的层数:节点的深度+1
树的高度: 根节点的高度

2.2. 二叉树(Binary Tree)
每个结点至多拥有两棵子树(即二叉树中不存在度大于2的结点),并且,二叉树的子树有左右之分,其次序不能任意颠倒
每个节点最多有两个“叉”,也就是两个子节点,分别是左子节点和右子节点
2.2.1. 二叉树的性质
1.若二叉树的层次从0开始,则在二叉树的第i层至多有2^i个结点(i>=0)
2.高度为k的二叉树最多有2^(k+1) - 1个结点(k>=-1)(空树的高度为-1)
3.对任何一棵二叉树,如果其叶子结点(度为0)数为m, 度为2的结点数为n, 则m = n + 1
二叉树又分为完美二叉树、完全二叉树、完满二叉树。

完美二叉树:换句话说、只要你有孩子,你就必然是有两个孩子。
2.2.2. 二叉树的遍历
前序遍历:(根->左->右) 对于树中的任意节点来说,先打印这个节点,然后再打印它的左子树,最后打印它的右子树。
中序遍历 :(左->根->右) 对于树中的任意节点来说,先打印它的左子树,然后再打印它本身,最后打印它的右子树。
后序遍历:(左->右->根) 对于树中的任意节点来说,先打印它的左子树,然后再打印它的右子树,最后打印这个节点本身。
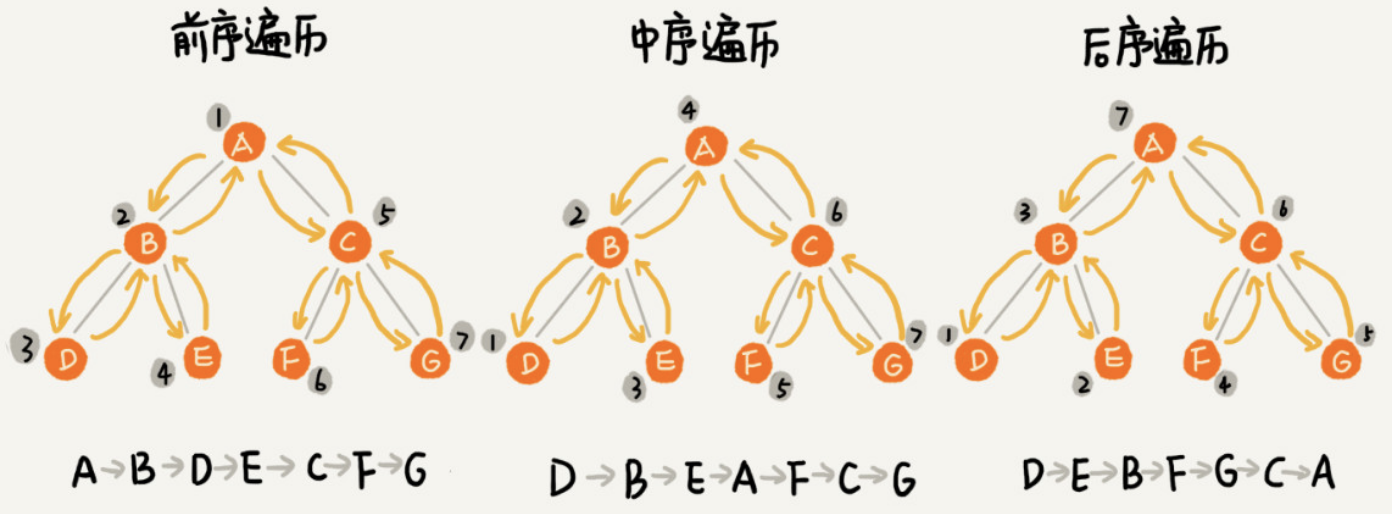
实际上,二叉树的前、中、后序遍历就是一个递归的过程。比如,前序遍历,其实就是先打印根节点,然后再递归地打印左子树,最后递归地打印右子树。
时间复杂度: 二叉树遍历的时间复杂度是 O(n)
递归实现二叉树的前序、中序、后序遍历
前序遍历:
public void preOrderRecur(Node root) {
if (root == null) {
return;
}
System.out.print(root.data + " -> ");
preOrderRecur(root.left);
preOrderRecur(root.right);
}
中序遍历:
public void midOrderRecur(Node root) {
if (root == null) {
return;
}
midOrderRecur(root.left);
System.out.print(root.data + " -> ");
midOrderRecur(root.right);
}
后序遍历:
public void posOrderRecur(Node root) {
if (root == null) {
return;
}
posOrderRecur(root.left);
posOrderRecur(root.right);
System.out.print(root.data + " -> ");
}
非递归(迭代)实现 前序、中序、后序遍历
栈实现前序遍历
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
Deque<TreeNode> deque = new ArrayDeque<>();
while(!deque.isEmpty() || root !=null){
while(root !=null){
res.add(root.val);
deque.offerLast(root);
root = root.left;
}
root = deque.pollLast();
root = root.right;
}
return res;
}
}
如何计算二叉树的层数
private int countLevel(TreeNode root) {
if (root == null) {
return 0;
}
return Math.max(countLevel(root.left), countLevel(root.right)) + 1;
}
二叉树的层序遍历
使用队列实现层序遍历
class Solution {
public static List<Integer> levelOrder(TreeNode root) {
Deque<TreeNode> deque = new LinkedList<>();
deque.offer(root);
List<Integer> res = new ArrayList<>();
while (!deque.isEmpty()) {
TreeNode levelRoot = deque.poll();
res.add(levelRoot.val);
if (levelRoot.left != null) {
deque.offer(levelRoot.left);
}
if (levelRoot.right != null) {
deque.offer(levelRoot.right);
}
}
return res;
}
}
构建一颗二叉树,DEBUG,看递归与迭代过程
package com.hellobike.rent.flink.etl;
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Deque;
import java.util.List;
/**
*
* 3
* / \
* 9 20
* / \
* 15 7
* @author gaohu08299
* @create $ ID: TestTreeNode, 2021-05-08 15:55 gaohu08299 Exp $
* @since 1.0.0
*/
public class TestTreeNode {
public static void main(String[] args) {
TreeNode t1 = new TreeNode(3);
TreeNode t2 = new TreeNode(9);
TreeNode t3 = new TreeNode(20);
TreeNode t4 = new TreeNode(15);
TreeNode t5 = new TreeNode(7);
t1.left = t2;
t1.right = t3;
t2.left = t4;
t2.right = t5;
List<Integer> integers = new TestTreeNode().preorderTraversal(t1);
System.out.println(integers);
}
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
Deque<TreeNode> deque = new ArrayDeque<>();
while(!deque.isEmpty() || root !=null){
while(root !=null){
res.add(root.val);
deque.offerLast(root);
root = root.left;
}
root = deque.pollLast();
root = root.right;
}
return res;
}
}
2.2.3. N叉树的层序遍历
利用队列进行广度优先搜索 关键代码
List<Integer> values = new ArrayList<>();
Deque<Node> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
Node nextNode = queue.poll();
values.add(nextNode.val);
for (Node child : nextNode.children) {
queue.add(child);
}
}
使用BFS实现的N叉树层次遍历
class Solution {
public List<List<Integer>> levelOrder(Node root) {
if (null == root) {
return new ArrayList<>();
}
List<List<Integer>> resp = new ArrayList<>();
Deque<Node> deque = new LinkedList<>();
deque.offer(root);
while (!deque.isEmpty()) {
List<Integer> ans = new ArrayList<>();
int size = deque.size();
for (int i = 0; i < size; i++) {
Node poll = deque.poll();
ans.add(poll.val);
List<Node> children = poll.children;
for (Node node : children) {
deque.offer(node);
}
//deque.addAll(poll.children);
}
resp.add(ans);
}
return resp;
}
}
二叉树的序列化
class Solution {
List<String> resp = new ArrayList<>();
public List<String> preorderTraversal(TreeNode root) {
if (null == root) {
return new ArrayList<>();
}
preOrder(root, new StringBuilder());
return resp;
}
public String preOrder(TreeNode root, StringBuilder sb) {
if (root == null) {
return "#";
}
sb.append(root.val).append(",").append(preOrder(root.left, new StringBuilder())).append(",").append(preOrder(root.right, new StringBuilder()));
resp.add(sb.toString());
return sb.toString();
}
}
二叉树序列化处理子树
class Solution {
Map<String,Integer> map = new HashMap<>();
List<TreeNode> resp = new ArrayList<>();
public List<TreeNode> findDuplicateSubtrees(TreeNode root) {
if(root == null){
return new ArrayList<>();
}
preOrderSerial(root,new StringBuilder());
return resp;
}
public String preOrderSerial(TreeNode root,StringBuilder sb){
if(root == null){
return "#";
}
sb.append(root.val).append(",").append(preOrderSerial(root.left,new StringBuilder())).append(",").append(preOrderSerial(root.right,new StringBuilder()));
map.put(sb.toString(),map.getOrDefault(sb.toString(),0)+1);
if(map.get(sb.toString()) == 2){
resp.add(root);
}
return sb.toString();
}
}
2.2.4. 二叉查找树
二叉查找树性质
- 任意节点左子树不为空,则左子树的值均小于根节点的值
- 任意节点右子树不为空,则右子树的值均大于根节点的值
- 任意节点的左右子树也分别是二叉查找树
- 没有键值相等的节点
局限性及应用
一个二叉查找树是由n个节点随机构成,所以,对于某些情况,二叉查找树会退化成一个有n个节点的线性链.
